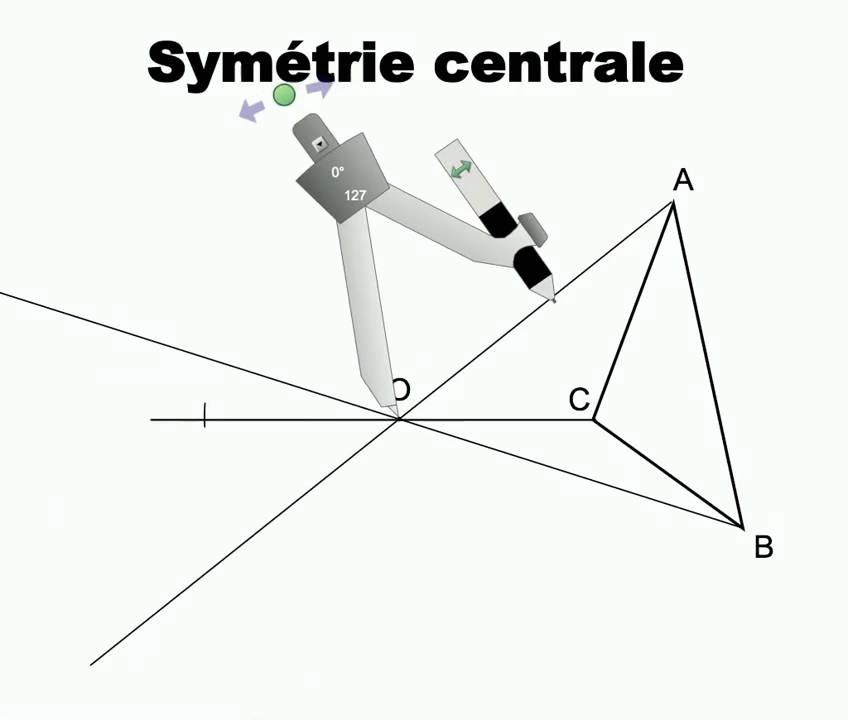
Chapitre 1 : Introduction à la symétrie centrale
La symétrie centrale est un concept géométrique fondamental qui consiste en une transformation qui laisse les points invariants par rapport à un centre donné. Elle est largement utilisée en mathématiques et en art. Comprendre la symétrie centrale est essentiel pour la résolution de problèmes géométriques et la création d’œuvres artistiques équilibrées. Dans cet article, nous explorerons en détail la symétrie centrale, en examinant les figures symétriques par rapport à un point, la symétrie d’un point, les propriétés de la symétrie centrale et le centre de symétrie d’une figure.
Chapitre 2 : La symétrie centrale
A) Figures symétriques par rapport à un point
Une figure est dite symétrique par rapport à un point si, pour tout point de la figure, il existe un autre point symétrique par rapport à ce point de symétrie. En d’autres termes, si une droite passant par le point de symétrie divise la figure en deux parties congruentes, alors la figure est symétrique par rapport à ce point.
Par exemple, le cercle est symétrique par rapport à son centre, car chaque point de sa circonférence a un point symétrique par rapport au centre.
B) Symétrique d’un point
Le symétrique d’un point par rapport à un centre de symétrie se trouve en prolongeant le segment de droite joignant le point au centre de symétrie de la même longueur de l’autre côté du centre de symétrie. Ainsi, le point et son symétrique sont équidistants du centre de symétrie.
Par exemple, si le point P a pour symétrique P’ par rapport au centre O, alors OP = OP’.
C) Propriétés de la symétrie centrale
La symétrie centrale possède plusieurs propriétés importantes. Par exemple, si A et B sont symétriques par rapport à un point O, alors le segment [AB] est parallèle à la droite passant par O et le milieu de [AB]. De plus, la symétrie centrale préserve les longueurs et les angles entre les éléments symétriques.
Il est essentiel de comprendre ces propriétés pour résoudre des problèmes géométriques complexes impliquant la symétrie centrale.
D) Centre de symétrie d’une figure
Le centre de symétrie d’une figure est le point à partir duquel toute symétrie centrale est définie. Pour identifier le centre de symétrie, on peut tracer des droites de symétrie et chercher le point qui laisse la figure invariante. Ce point est le centre de symétrie de la figure.
Par exemple, un rectangle a son centre de symétrie à l’intersection de ses diagonales, tandis qu’un cercle a son centre de symétrie à son centre géométrique.
Vous pourriez aimer:
Si vous avez trouvé cet article intéressant, vous pourriez également aimer notre article sur les transformations géométriques, qui explore en détail les translations, rotations et homothéties.
| Chapitre | Contenu |
|---|---|
| A) Figures symétriques par rapport à un point | Concept de symétrie par rapport à un point et exemples. |
| B) Symétrique d’un point | Procédé pour trouver le symétrique d’un point par rapport à un centre de symétrie. |
| C) Propriétés de la symétrie centrale | Principales propriétés de la symétrie centrale et leur application. |
| D) Centre de symétrie d’une figure | Méthodes pour identifier le centre de symétrie d’une figure géométrique. |
Leçons apprises
En comprenant la symétrie centrale, vous serez en mesure de résoudre des problèmes géométriques complexes et de créer des œuvres artistiques équilibrées. La maîtrise de ce concept est cruciale pour de nombreuses applications pratiques et esthétiques.
FAQ
Comment réaliser une symétrie centrale ?
Pour réaliser une symétrie centrale, il faut d’abord choisir un point qui servira de centre de symétrie. Ensuite, chaque point de la figure initiale doit être relié à un nouveau point situé de l’autre côté du centre de symétrie, à une distance égale. C’est comme si on ‘pliait’ la figure sur le point central.
Comment faire de la symétrie ?
La réalisation de la symétrie consiste à créer un équilibre ou une correspondance entre les différentes parties d’un objet. Concrètement, cela peut consister à diviser un dessin en deux moitiés identiques le long d’un axe, à reproduire une figure de la même manière dans des directions opposées, ou encore à disposer les éléments d’une structure de manière à obtenir une correspondance constante lorsqu’on la fait pivoter ou se réfléchir.
Comment expliquer la symétrie centrale ?
La symétrie centrale est une transformation géométrique où chaque point d’une figure est transposé à une distance égale de part et d’autre d’un point central appelé centre de symétrie. Ainsi, l’image obtenue est une réflexion de la figure originale par rapport à ce point central.
Comment tracer l’image d’un point par une symétrie centrale ?
Pour tracer l’image d’un point par une symétrie centrale, on relie le point au centre de symétrie. On prolonge cette ligne de la même distance de l’autre côté du centre. Le point d’arrivée est l’image du point initial par la symétrie centrale.